Le flambage des structures en béton
Les structures en béton, éléments fondamentaux du génie civil et de la mécanique, sont constamment exposées à des contraintes diverses qui peuvent engendrer des phénomènes préoccupants, dont le redouté flambage.
Au cœur de cette problématique, SODIAGS, un bureau d’études spécialisé dans les diagnostics structurels, ainsi que dans le calcul de capacité portante et le renforcement des structures, se positionne comme un acteur essentiel dans la compréhension et la résolution des défis liés au flambage.

Exploration approfondie du flambage et son analyse via la formule d'Euler :
Le flambage, également dénommé flambement, est un phénomène physique qui s’inscrit dans les principes de la résistance des matériaux. Lorsqu’une structure est soumise à une compression dans le sens de sa longueur, elle présente une propension à fléchir perpendiculairement à l’axe de la force appliquée, en raison d’une instabilité élastique. La facilité avec laquelle la structure, telle qu’une poutre, fléchit dépend de sa longueur et de sa finesse, ainsi que d’autres variables, comme le système de fixation aux points de compression.
Le calcul du flambage repose sur la formule d’Euler, qui permet d’évaluer la charge critique à partir de laquelle la structure risque de se rompre.
F = ?²EI/(l_k^²)
Cette formule intègre des paramètres tels que le module de Young du matériau (E), le moment quadratique de la structure (I), et la longueur de flambement de la poutre (l_k).

Le module de Young, exprimé en MPa dans le Système International, est une constante élastique qui lie la contrainte à la déformation d’un matériau homogène isotrope. Ce coefficient caractérise la raideur du matériau. À contrainte égale, un matériau doté d’un module d’élasticité élevé subira une déformation moindre qu’un matériau ayant un module d’élasticité plus faible. Il convient de noter que le module d’élasticité peut varier en fonction du mode de chargement, que ce soit en traction, compression ou flexion.
Dans le cas d’un composite orthotrope, la relation entre déformation et contrainte est déterminée par trois « modules d’élasticité » distincts selon les trois axes, avec une relation complète exprimée sous forme matricielle. Pour déterminer le module d’élasticité E d’un matériau isotrope, un essai de traction est réalisé, et la pente de la courbe linéaire de contrainte en fonction de la déformation correspond au module d’élasticité en traction du matériau.
Distinction entre flambage et courbure des colonnes
Flambage des Colonnes
Le flambage est un phénomène qui se produit lorsque, pour des raisons d’irrégularités de la matière et des forces appliquées, une colonne se met à fléchir sous une charge parallèle à son axe. En d’autres termes, c’est un problème de flexion. Le flambage est particulièrement important dans la conception des structures, car il peut entraîner la défaillance d’une colonne si elle n’est pas correctement dimensionnée.
Voici quelques points clés concernant le flambage des colonnes :
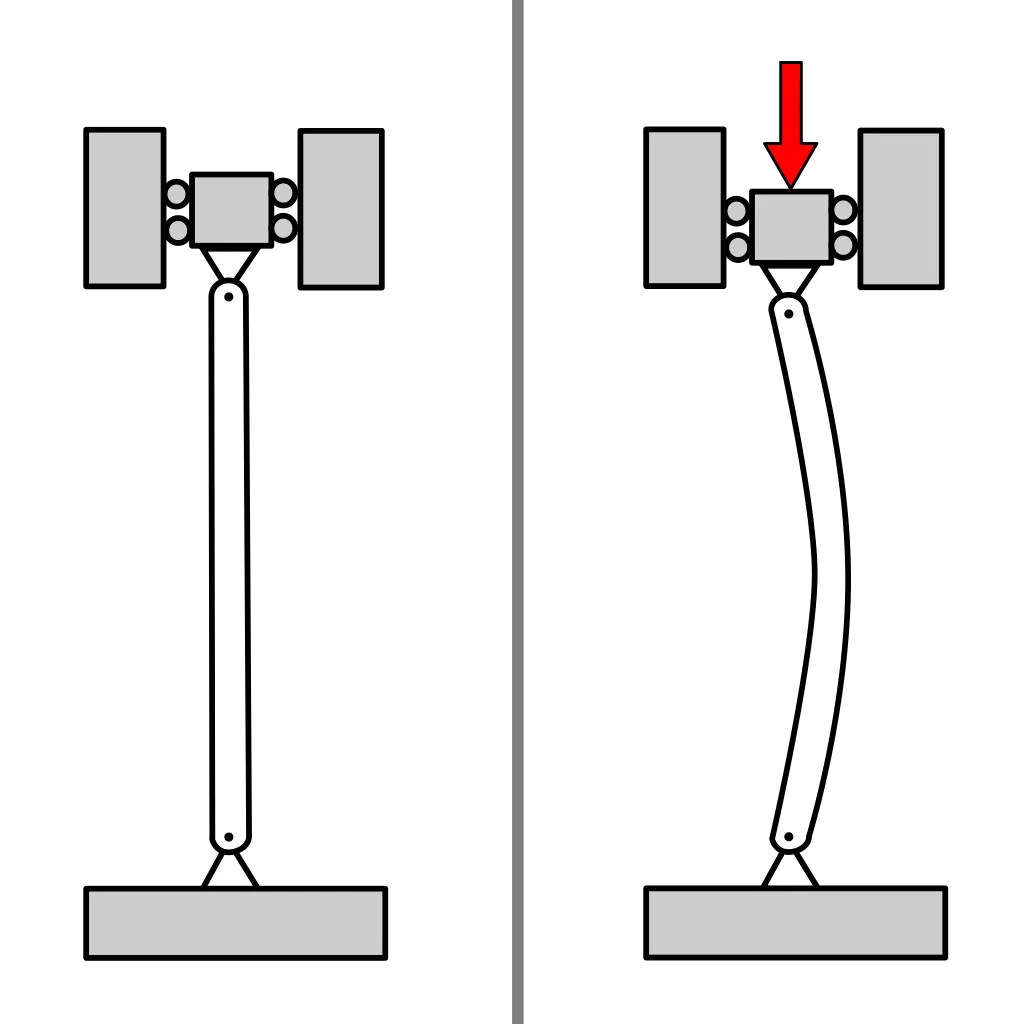
- Longueur de Flambage (Lfl) : La longueur de flambage d’une colonne dépend de sa longueur réelle ainsi que de la nature de ses appuis (encastrés, rotulés, etc.). Plus la colonne est élancée, plus la charge critique de flambage diminue.
- Inertie (I) : L’inertie du profilé joue un rôle crucial dans le flambage. Une section transversale avec une inertie plus grande est plus résistante au flambage.
- Module de Young (E) : Le module de Young du matériau de la colonne affecte également sa capacité à résister au flambage. Par exemple, une colonne en acier peut supporter une charge plus importante qu’une colonne en bois de même géométrie.
Courbure des Colonnes
La courbure des colonnes, quant à elle, se produit lorsque la contrainte d’un élément dépasse la limite d’élasticité du matériau. Contrairement au flambage, la courbure peut se produire avant que la flexion ne se manifeste. Cela signifie que la colonne commence à se déformer sans nécessairement fléchir complètement.
En résumé, le flambage est spécifiquement lié à la flexion sous une charge axiale, tandis que la courbure peut se produire avant même que la flexion ne se manifeste.
En somme, le flambage d’une colonne survient lorsque des charges axiales de compression induisent une déviation latérale, potentiellement conduisant à une défaillance abrupte. En revanche, la courbure des colonnes est une déformation progressive, ne conduisant pas nécessairement à une défaillance immédiate. SODIAGS souligne l’importance de consulter un ingénieur en structure agréé pour évaluer les risques liés au flambage ou à la courbure des colonnes, mettant en avant la nécessité d’une approche spécialisée.
Exploration du rapport d'élancement et son incidence sur la stabilité des colonnes :
Facteurs Influant sur la charge critique
La charge critique d’une colonne est soumise à l’influence de multiples facteurs tels que les conditions d’appui, la longueur, la coupe transversale, le matériau et la forme. SODIAGS utilise des méthodes avancées, telles que la formule parabolique de Johnson ou la formule d’Euler pour le flambage des poteaux, afin de calculer la charge critique. Le BET insiste sur la nécessité de considérer ces facteurs pour une évaluation précise et propose des interventions sur mesure. SODIAGS se positionne comme un expert, mettant en avant l’importance d’une approche holistique pour garantir l’intégrité des structures.
La formule parabolique de Johnson
La formule parabolique de Johnson constitue un modèle empirique essentiel en ingénierie structurelle, dédié à évaluer la contrainte critique de flambement d’une colonne. Conçue par J. B. Johnson, elle se présente comme une alternative à la célèbre formule d’Euler, spécifiquement adaptée aux colonnes caractérisées par un faible rapport d’élancement. Sa représentation mathématique est la suivante :
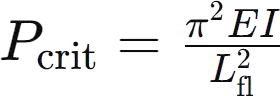
Dans cette équation :
- 𝑃critPcrit désigne la charge seuil déclenchant le flambement.
- 𝐸E représente le module de Young du matériau.
- 𝐼I correspond à l’inertie du profilé.
- 𝐿flLfl est la longueur critique de flambement de la colonne.
La formule parabolique de Johnson réalise une interpolation entre la contrainte de limite d’élasticité du matériau et la contrainte critique de flambement fournie par la formule d’Euler. Son principe repose sur la création d’une nouvelle frontière de défaillance, obtenue en ajustant une parabole à la courbe de défaillance pour le flambement d’Euler.
Préservez la stabilité de vos structures en béton avec SODIAGS ! Consultez nos experts pour une évaluation approfondie du risque de flambage et bénéficiez de solutions sur mesure. Assurons ensemble la durabilité de vos projets. Contactez-nous maintenant pour une expertise fiable et proactive.

Partagez cet article sur le réseau de votre choix : & n'hésitez pas à laisser un commentaire :



